Answer-Getting and: Analyzing Student Mistakes
See previously: Some Thoughts on Interventions & Answer Getting
So here’s something I started doing in an effort to keep students more engaged in problems and less focused on the most direct route to getting to the answer: I started having them analyze their own mistakes. This isn’t new – Kelly O’Shea’s idea for The Mistake Game has been around for a long time and it was a definite inspiration for my explicit focus on mistakes. But, I didn’t think I could jump right into having my students create their own mistakes – here’s why:
- Generating mistakes requires you to be confident enough that you could solve the problem without a mistake in the first place. My students don’t start out having this confidence – I needed to work on building it first.
- Generating mistakes requires you to care about how you got your answer, not what the final answer ends up being. Its possible to generate two mistakes which, as the problem progresses, cancel each other out and give the final answer. As a teacher, I see this as an incorrect problem even though the final answer is correct. Students with the Answer-Getting Mindset will see this as correct because the final answer is correct – learning to see the problem as an entire body of work is something that I need to train them to do before purposefully making mistakes has any meaning to them.
- Generating mistakes requires me to ask a “how/why” question rather than a “what” question. Answer-Getting is all about what: “What is the answer?”, “What is the next step?”. How and Why questions focus on process: “How did you get from this step to this step?”, “Why are you allowed to do this?”, “Why can’t I do this instead?”, “How would you explain this process in words rather than numbers or symbols?”. In general, I want to be asking more how/why questions rather than what questions.
Analyzing Mistakes
At the start of the year, all of my students took a pretest that covered basic arithmetic, solving basic equations, and basic graphing skills. As the year progressed and I had begun to explicitly teach these skills and build confidence, I would eventually come to a lesson where we revisited these tests. To do this, I took lots and lots of pictures of these initial tests (without any student names showing):
Students would walk into class and see a single picture on the board. They wonder whose mistake it is, which gives some social buy-in. Each person wants to be the first person to find the mistake, which gives some competitive buy-in. As class starts, I ask them: Where is the mistake? At first, students tell me the answer is wrong (which is true). Then they try to work it out themselves and give me the right answer – but, since we’re still in the middle of mastering these skills, these answers still aren’t very reliable. Usually there are multiple answers, so I let them debate for a while. Then I interrupt:
“You’re not answering my question. I asked ‘Where is the Mistake?’, not ‘What is the Answer?’. I don’t care what the answer is. I care where they made a mistake”
I let that sink in for a minute because, for someone with an Answer-Getting mindset, this stops them cold. A teacher just told them that they don’t care about an answer. This either makes this class new and intriguing or new and terrifying. Either way, we’re gonna work through this.
“I want to get to the point where I can circle the part of the problem where this student made a mistake. This means I need to look at each line of their work and ask myself ‘Do I understand what they did?’ and then ‘Was it the right step? Did they get the right number?'”
And we’re off. I guide them through looking at each step of the work. I ask them to describe that this person did from one line to the next, ask if this was an okay thing to do, then verify that they got the right numbers. We talk about how not showing our work can make it harder to find mistakes. I show them how to circle the individual step of the problem that is incorrect. We look at the next mistake, which is the same starting problem but with a different mistake somewhere in there. Isn’t it interesting how one problem can have so many different mistakes? Is this a mistake you might have made? Are there multiple mistakes?
For students who’ve built up walls around these problems in the form of dismissal and anger and solve-as-fast-as-I-can, they tend to give these problems a second-chance because they’re not actually being asked to solve the problem. This slight change in what I’m asking them to do is enough for them to engage with the work even if working out the problem itself would have been a motivational challenge. For students who’ve built up walls around these problems in the form of apathy and not-trying and fear of failure, I found that they start to quietly participate in these discussions because this type of question is new and doesn’t have any past stigmas of failure associated with it. Either way, I have students genuinely engaging with a set of problems and, hopefully, feeling successful as they do it.
Full Disclosure: I’m leaving out all the important work that happens in the classroom as we discuss these – the graceful handling of student pushback; the subtle encouraging and guiding of students thoughts; the questioning strategies and No Opt-Out mentality that I have; etc etc. There’s lots of other explicit and implicit things that need to happen, but they’re the things that differ from teacher to teacher.
After doing this as a class, I would give students a problem set in two-columns. The left-column had a problem and a hand-written solution that intentionally had a mistake. The right-column had the same problem and a space for work. Students needed to find the mistake and circle it in the left column, then solve the problem correctly in the right column.
Push-Back Against Answer-Getting
- Part of the Answer-Getting mindset is avoiding mistakes because they’re bad. Explicitly analyzing mistakes and getting exciting about them starts to remove a lot of that stigma and fear. This is all over Math & Science Education research – the idea of normalizing mistakes and internalizing it as growth versus verification – and this is how I managed to do that in my classroom.
- Students get practice explaining their steps and discussing how to get to answers versus what is the answer. There are lots of students who make little mistakes leading up to answers, but are actually very capable of explaining their thinking out loud. For some students, this oral explanation needs to become part of their problem-solving toolkit. For these students, they start to realize that all their steps may be correct even if their final answer isn’t, which is an easier problem to fix and helps to build confidence.
- When students get a problem incorrect, it starts to become normal for me to ask them to find their mistake. In doing this, students begin to see value in showing their work. And not just because the teacher said so – because it makes it easier to retrace their thought process and identify their mistakes. This is one of the first times in the class that I say to students “I think you should do this because it’s helpful to you, not because I’m being mean and want you to do extra work”, and they begin to believe me.
- This is one of the first times where I’ve made it explicit that there’s more to math than just getting the right answer. Which, in terms of motivation and attitude towards math, may be something my students need to hear.
A Few Other Things
Here are all the Integer Mistakes.
Here are all the Algebra Mistakes.
Here is Michael Pershan’s Math Mistakes website, which has tons of other mistakes to peruse.
The same day I published these thoughts, Michael Pershan publishes his thoughts on How He Gives Back Quizzes. Embedded in this post is his method of displaying mistakes as a way to generate discussions as part of quiz feedback – if you enjoyed reading this, try reading his ideas too.
Even with all of these resources, I highly recommend finding a way to naturally generate your own student mistakes to analyze. The buy-in this creates from students – “Who’s is that? Is it mine? Is it _______ from 4th period?” is important, and the fact that we’re normalizing our own mistakes is important.
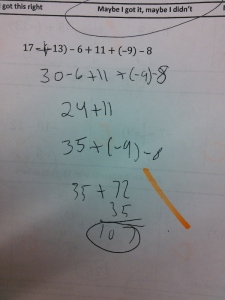
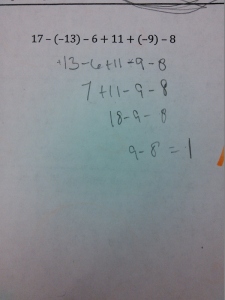
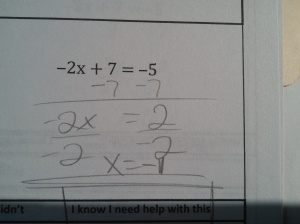
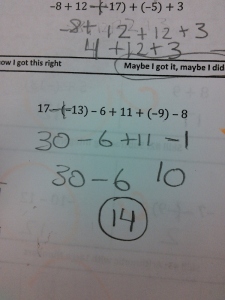
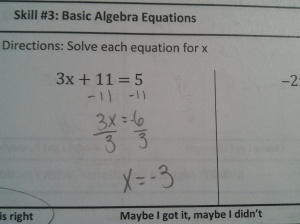
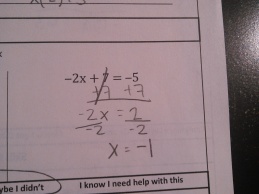

I love this and so value all of your posts. My colleague and I have started giving out error analysis sheets every time we return a graded quiz. We copy actual student work (with the common mistakes we found) from the quiz and the students have to do an error analysis and then write out the correct solution.
What we’ve found is that — for once — the students are actually looking at their returned, graded quizzes. Giving them time in class to do this error analysis gives the kid a chance to think about or ask me about his mistake or misconception.
This also allows the students to see what quality “showing of work” looks like.
Would you be willing to share the pretest you gave your students with us? I want to do something like this next year with my Algebra 1 and Algebra 2 classes. Transitioning to CCSS will leave us little time to reteach these concepts from scratch, so I’m hoping that doing error analysis will help correct students’ misunderstandings. Thanks in advance!
Hi Sarah,
They’re in here towards the top: https://mathymcmatherson.wordpress.com/things-ive-made/
Hope they help
-Mathy
Awesome! Thanks for the link!
I love the emphasis on finding the first mistake. That’s makes sense now that you’ve said it as it’s easy to get bogged down in how a mistake played out or how they didn’t do it ‘my way.’ I can’t wait to try this.
Your comment reminded me: the “They didn’t do it my way” discussion was really interesting for the algebra mistakes. A lot of students wanted to say that part of a problem was a ‘mistake’ just because the person solved the problem differently than they would have. Parsing through that was really valuable and helped emphasize the correct ‘rules of algebra’ versus the correct ‘answer-getting way to solve an algebra problem’.
Many teachers have found ways to engage their students in this manner. It really helps them engage and work with their peers. Anonymizing the mistake limits the peer pressure so they try harder, knowing it will no come back on them as quickly.